AP Computer Science Sorting Test

(Are you a Gryffindor?)

0. (0 points) NAME________________________________________ PERIOD_________

INSTRUCTIONS

• Put your name on the test. Failure to do so will result in a loss of one point. (Let's face it, if you don't know your name, you probably have bigger problems than this test.)
• This test is closed book. No computer, no friends, just you and the test.
• Where possible, SHOW YOUR WORK! I don’t know how to assign partial credit to the void.
• Don't panic. It's just a test.

1. (5 points in three parts) Consider the following sorting method:

    public static void mystery(int[] a) {
        for (int i = 1; i < a.length; i++) {
            int j = i;
            int current = a[i];
            while (j > 0 && current < a[j-1]) {
                a[j] = a[j-1];
                j--;
            }
            a[j] = current;
        }
    }

1A. (1 point) What is the name of this sorting method? (Circle the correct answer.)

Bubble Sort        Insertion Sort        Selection Sort        Heap Sort        Quick Sort        Merge Sort

1B. (3 points; 1 for order of growth, 2 points for explanation) What is the order of growth of this sorting method? Explain why. (Let n be the number of elements in the array for the purpose of your explanation.)

This is insertion sort. Note that indexing starts with i = 1; the 0th position is sorted to begin. The element at a[i] is stored in current and the while loop shifts elements greater than current to the right until the place to insert current is established.

1C. (1 point) Consider the line of code:

while (j > 0 && a[j-1] > a[j])

Why was it written this way instead of the below line of code?

while (a[j-1] > a[j] && j > 0)

Logical AND works left to right. If the check to see if j == 0 is not performed before comparing elements in the array, then a[-1] will result in an ArrayIndexOutOfBounds exception being thrown.

One of these tables is the result of quick sort, the other is a result of insertion sort.

2A. (3 points) Which table could represent the behavior of quick sort? Which one is insertion sort? Explain using orders of growth.

The first example can be described by f(n) = .04 * n². The second can be described (roughly) as g(n) = .1 * (nlog₂n). Insertion sort is O(n²) while quicksort is an O(nlog₂n). It is useful to remember that log₂1024 is 10 for estimation purposes.





2B. (2 points) A reasonable function for describing the below table is time = 5nlogn + 4000.

Write mathematical functions of the form time = f(n) for the sorts in TABLE 1 and TABLE 2.

Repeating the analysis from above, the first example can be described by f(n) = .04 * n². The second can be described (roughly) as g(n) = .1 * (nlog₂n). Insertion sort is O(n²) while quicksort is an O(nlog₂n).

3. (5 points)

Given:

int[] nums = {5, 3, 9, 6, 4, 2, 8, 0, 7, 1};

For all problems, assume that the sorts will be in ascending order (i.e., smallest to biggest).

A. What will nums look like after two passes of bubble sort?

       initially:

after pass 1:

after pass 2:

B. What will nums look like after two passes of selection sort?

       initially:

after pass 1:

after pass 2:

C. What would nums look like if, as seen in class, it were built into a maxheap to prepare a heap sort?

                      BEFORE BUILDING HEAP                                      AFTER HEAP BUILT

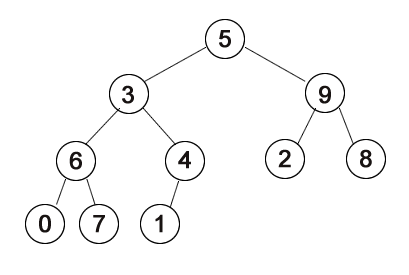
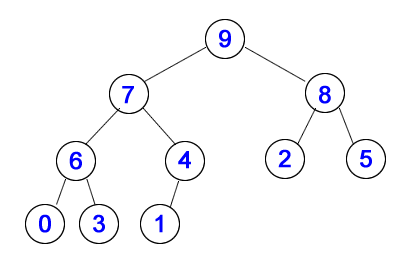
A maxheap means that the datum at every node is larger than the data of its children. Building a maxheap works right-to-left, bottom-to-top, in this order:

4. (5 points) Write mergesort in Java for ArrayList<Comparable> by filling in the blanks. To assist you, mergesort as fully written in Scheme is given to you. So is a substantial portion of the ArrayList abstraction. A diagram of how mergesort works is shown below.

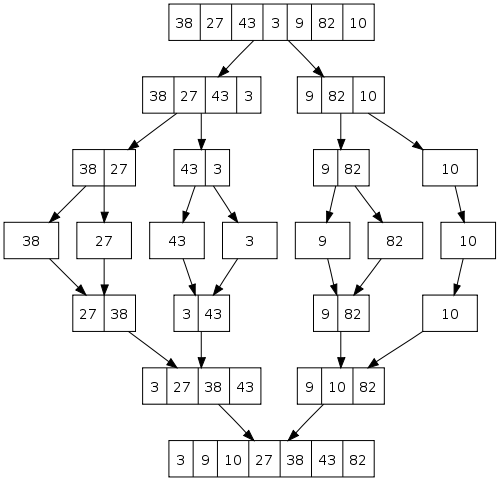
Mergesort works as follows (from Wikipedia page on Mergesort):

1. If the list is of length 0 or 1, then it is already sorted. Otherwise:
2. Divide the unsorted list into two sublists of about half the size.
3. Sort each sublist recursively by re-applying merge sort.
4. Merge the two sublists back into one sorted list.

Here is the mergesort method. You will need to write left, right, and merge to make it work.

	public static ArrayList<Comparable> mergesort(ArrayList<Comparable> alist) {
		if (alist.size() < 2)
			return alist;
		else {
			return merge(mergesort(leftHalf(alist)), mergesort(rightHalf(alist)));
		}
	}

4A. (1 point) Write left, which takes an ArrayList<Comparable> as input and returns an ArrayList<Comparable> that contains the first half of the input. If the number of elements in the input list is odd, then the middle element should be included in left.

   private static ArrayList<Comparable> leftHalf(ArrayList<Comparable> alist) {
		ArrayList<Comparable> tmp = new ArrayList<Comparable>();    // Empty ArrayList
		int numElements = (int) Math.ceil(alist.size() / 2.0);             // Math.ceil rounds up

		for (int i = 0; i < numElements; i++) {

			tmp.add(alist.get(i));  // the elements of the lower half of possible indices are put into tmp

		}

		return tmp;
	}

4B. (1 point) Write right, which takes an ArrayList<Comparable> as input and returns an ArrayList<Comparable> that contains the second half of the input. If the number of elements in the input list is odd, then the middle element should NOT be included in right.

	private static ArrayList<Comparable> rightHalf(ArrayList<Comparable> alist) {
		int index = (int) Math.ceil(alist.size() / 2.0);  // start copying from position index
		int numElements = alist.size() / 2;

		ArrayList<Comparable> tmp = new ArrayList<Comparable>();

		for (int i = 0; i < numElements; i++) {

			tmp.add(alist.get(index + i));  // the elements of the upper half of possible indices are put into tmp

		}
		return tmp;

	}

4C. (3 points) Write merge which takes two ArrayList<Comparable>s in ascending order (as determined by Comparable) as its inputs and returns an ArrayList<Comparable> containing the elements of both inputs in ascending order.

	private static ArrayList<Comparable> merge(ArrayList<Comparable> alist1, ArrayList<Comparable> alist2) {
		ArrayList<Comparable> tmp = new ArrayList<Comparable>();

		while (alist1.size() > 0 && alist2.size() > 0) {

			// Find the smaller of the front elements in each list.  Whichever that is, it gets added to tmp.
			// Two things of note:
			// * remove() in an ArrayList returns the object being removed
			// * This process is repeated until one of the list no longer contains elements

			if (alist1.get(0).compareTo(alist2.get(0)) < 0) {

				tmp.add(alist1.remove(0));

			} else {

				tmp.add(alist2.remove(0));

			}
		}

		// One of the two lists is empty.  The while loop on the list that is empty does zero iterations.
		// The while loop on the list containing elements adds them to the end of tmp, completing the merging
		// of the two input lists.

		while (alist1.size() > 0)

			tmp.add(alist1.remove(0));

		while (alist2.size() > 0)

			tmp.add(alist2.remove(0));

		return tmp;
	}