AP CS Programming Test #3

0. (0 points) NAME________________________________________ PERIOD_________

INSTRUCTIONS

• Put your name on the test. Failure to do so will result in a loss of one point. (Let's face it, if you don't know your name, you probably have bigger problems than this test.)
• This test is closed book. No friends, no computer, just you, your brain, your test, and your pencil.
• Where possible, SHOW YOUR WORK! I don’t know how to assign partial credit to the void.
• Don't panic. It's just a test.

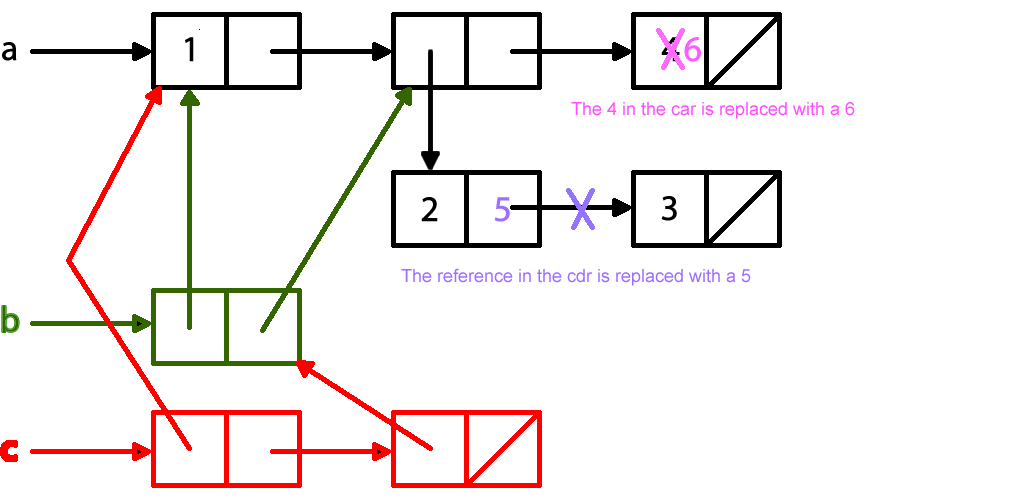
1. (5 points; 1 point per line of code) Suppose that the following five lines of Scheme code are executed. Draw the box-and-pointer diagram that results for each line of code.

(Draw one diagram for all five lines.)

(define a '(1 (2 3) 4))

(define b (cons a (cdr a)))

(define c (list a b))

(set-cdr! (cadr b) 5)

(set-car! (cddar c) 6)

(1/2 point bonus) What is the output of (cadr a)?

(2 . 5)

2. (3 points) Write Scheme code that will produce the following environment diagram:

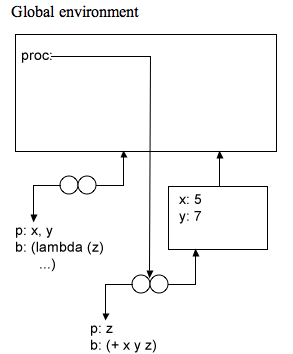
Note that proc is a procedure that takes one input, z, but that procedure must be inside a let (the unnamed procedure on the left and the corresponding frame that gets created when it is called immediately). So we get:

(define proc
  (let ((x 5)
        (y 7))
    (lambda (z) (+ x y z))))
  

3. (8 points) Exercise 3.22 from the book.

Instead of representing a queue as a pair of pointers, we can build a queue as a procedure with local state. The local state will consist of pointers to the beginning and the end of an ordinary list. Thus, the make-queue procedure will have the form

(define (make-queue)
  (let ((front-ptr ...)
        (rear-ptr ...))
     <definitions of internal procedures>
     (define (dispatch m) ...)
     dispatch))

Complete the definition of make-queue and provide implementations of the queue operations using this representation by filling in the blanks.

(define (make-queue)
  (let ((front-ptr '())
        (rear-ptr '()))
    (define (empty?)

      (null? front-ptr))  ; Can actually ignore rear-ptr; need to set rear-ptr to '() in
                          ; delete! if we want to include it here.

    (define (insert! datum)
      (let ((new-pair (cons datum '())))  ; For some reason, some people never used new-pair
       
        (cond ((empty?) (set! front-ptr new-pair)

                        (set! rear-ptr new-pair))

              (else (set-cdr! rear-ptr new-pair)

                    (set! rear-ptr new-pair)))))

    (define (delete!)  ; Must return the first element of the queue in addition
                       ; to deleting it from the queue
      (cond ((empty?) (error "Nothing in queue to delete!"))

            (else (let ((datum (car front-ptr)))  ; could also use (peek)

                    (set! front-ptr (cdr front-ptr))

                    datum))))

    (define (peek)
      (cond ((empty?) (error "Nothing in queue to return!"))

            (else (car front-ptr))))

    (define (dispatch m)
      (cond ((eq? m 'insert!) insert!)
            ((eq? m 'delete!) delete!)
            ((eq? m 'peek) peek)))

    dispatch))

4. (4 points, 1/2 point per blank) Consider the following code:

(define (make-thing)
  (let ((a 0)
        (b 1))
    (define (next)
      (let ((return b)
            (c (+ a b)))
        (set! a b)
        (set! b c)
        return))
    (lambda (msg)
      (cond ((eq? msg 'next) next)
            (else (error "?"))))))

(1/2 point per blank) In each blank, fill in what will be returned for that line of code. (The code sequence matters.)

> (define x (make-thing))

> (x 'next)       #<procedure>

> ((x 'next))     1

> ((x 'next))     1

> ((x 'next))     2

> ((x 'next))     3

> ((x 'next))     5

> ((x 'next))     8

In English, what would a good name for make-thing be? make-fibonacci